SOAL TRANSFORMASI DAN PENYELESAIANNYA

 GATHAN DARMAWAN

1. Tentukan koordinat titik A jika A’ (13, -20) merupakan bayangan titik A karena translasi B (10, -7), yaitu:

Pembahasan : 

Misal A = (x, y), maka

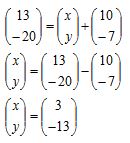
Jadi, koordinat titik A adalah (3, -13).

2. Diketahui B’(8, 4) merupakan bayangan titik B(x, y) yang dirotasikan pada pusat (0, 0) sebersar 90o. Berapakah nilai 2x + y?

Pembahasan : 

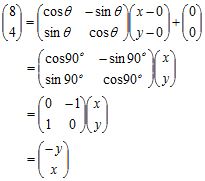
Diperoleh x = 4 dan y = -8. Maka:

2x + y = 2 (4) + (-8)

2x + y = 8 – 8

2x + y = 0

Jadi, nilai 2x + y adalah 0.

3.  Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

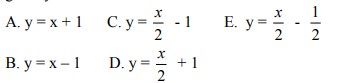
Jawaban : C

Pembahasan : 

4. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah …. 

A. y = x² – 2x – 3 

B. y = x² – 2x + 3

C. y = x² + 2x + 3

D. x = y² – 2y – 3

E. x = y² + 2y + 3

Jawaban : D

Pembahasan : 

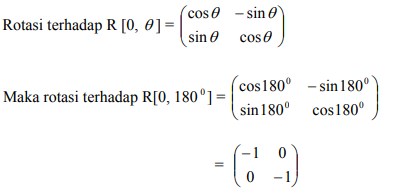
Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.

pencerminan terhadap garis y = -x

5. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks  adalah…. 

A. x² + y² – 6x – 4y- 3 = 0

B. X² + y² – 6x + 4y- 3 = 0

C. x² + y² + 6x – 4y- 3 = 0

D. x² + y² – 4x + 6y- 3 = 0

E. x² + y² + 4x – 6y+ 3 = 0

Jawaban : A

Pembahasan : 

6. T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan 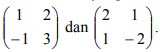Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…

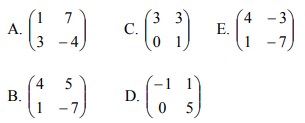
Jawaban : E

Pembahasan : 

7. Ditentukan matriks transformasi .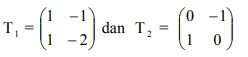 Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah…. 

A. (-4,3)

B. (-3,4)

C. (3,4)

D. (4,3)

E. (3,-4)

Jawaban : A

Pembahasan : 

8. Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks   kemudian dilanjutkan dengan matriks 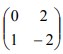adalah…

A. x + 2y + 3 = 0 

B. x + 2y – 3 = 0 

C. 8x – 19y + 3 = 0

D. 13x + 11y + 9 = 0

E. 13x + 11y – 9 = 0

Jawaban : E

Pembahasan : 

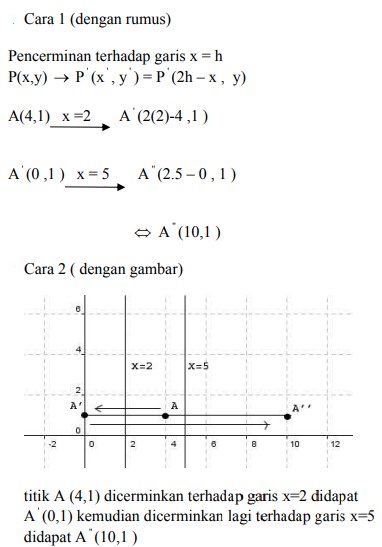
9. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik…. 

A. A” (8,5) 

B. A” (10,1)

C. A” (8,1) 

D. A” (4,5)

E. A” (20,2)

Jawaban : B

Pembahasan : 

10. T1 adalah transformasi yang bersesuaian dengan matriks 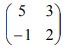 dan T2 adalah transformasi yang bersesuaian dengan matriks  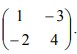Bayangan A (m,n) oleh transformasi T1 o T2 adalah (-9,7). Nilai m+n sama dengan…

A. 4

B. 5

C. 6

D. 7

E. 8 

Jawaban : B

Pembahasan : 

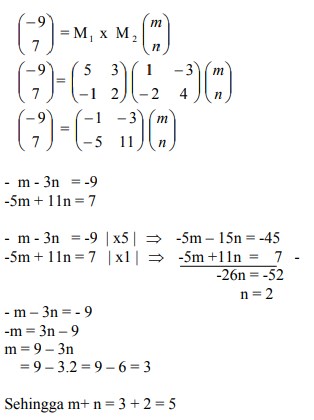
`11. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…

A. A” (-1,-2), B” (1,6) dan C” (-3,-5)

B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)

C. A” (1,-2), B” (-1,6) dan C” (-3,5)

D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)

E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan : 

12. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…

A. 3y + x² – 9x + 18 = 0

B. 3y – x² + 9x – 18 = 0

C. 3y – x² + 9x + 18 = 0

D. 3y + x² + 9x + 18 = 0

E. y + x² + 9x – 18 = 0 

Jawaban : A

Pembahasan : 

pencerminan terhadap sumbu x:

P ( x , y ) → P ‘ ( x , – y )

Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :

[O, k] : P(x,y) → P'(kx, ky)

[O,3k] : P(x,y) → P'(3x, 3y)

pencerminan terhadap sumbu x dilanjutkan dilatasai
dengan pusat O dan factor skala 3 :

P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

13. Luas bayangan persegipanjang PQRS dengan

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…

A. 36

B. 48

C.72

D. 96

E. 108

Jawaban : E

Pembahasan : 

dilatasi [0,3] :

[O,3k] : P(x,y) → P ‘(3x, 3y)

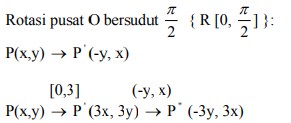
Sehingga :

P(x,y) → P” (-3y, 3x)

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

P(-1,2) → P” (-6,-3)

Q(3,2) → Q” (-6,9)

R (3,-1) → R” (3,9)

S(-1,-1) → S” (3,-3)

Buat sketsa gambarnya:

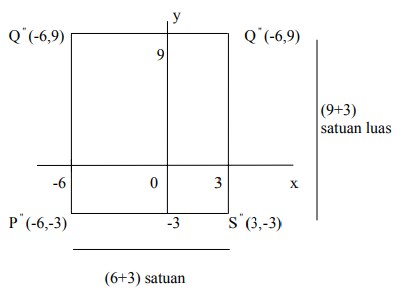
Sehingga luas transformasinya adalah :

Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas

14. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 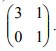 Luas bangun hasil transformasi segitiga ABC adalah….

A. 56 satuan luas 

B. 36 satuan luas

C. 28 satuan luas

D. 24 satuan luas 

E. 18 satuan luas

Jawaban : E

Pembahasan : 

misalkan T = 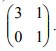maka

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3

luas ∆ ABC :

buat sketsa gambar :

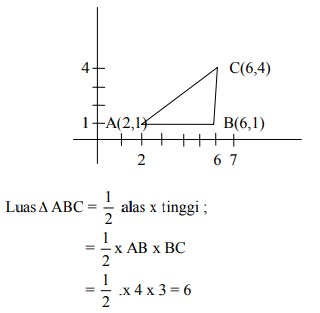
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC

= 3 x 6 = 18 satuan luas

15. Tentukan bayangan lingkaran (x-3)2 + (y+1)2 = 4 jika ditranslasikan 

 

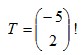
a. 5

b. 4

c. 3

d. 2

e. 1

Jawaban : B

Pembahasan : 

Ambil sembarang titik P(a,b) pada lingkaran (x-3)2 + (y+1)2 = 4 sehingga diperoleh (a-3)2 + (b+1)2 = 4

16. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!

Jawaban :  

Pembahasan : 

17. Jika titik A(15,8) dicerminkan terhadap garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….

Jawaban : 

Pembahasan : 

18. Titik A(a,b) dicerminkan terhadap garis x=2 menghasilkan bayangan titik A’(0,2), maka nilai (a,b) berturut-turut adalah….

a. 2 , 4

b. 4 , 2 

c. 2 , 2

d. 3 , 1

e. 1 , 3

Jawaban : B

Pembahasan : 

19. Titik A’(-16,24) merupakan bayangan dari titik A(x,y) yang didilatasikan dengan pusat O(0,0) dan faktor skala -4. Koordinat titik A adalah….

Jawaban : 

Pembahasan : 

20. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu x!

Jawaban : 

Pembahasan : 

21. Tentukan persamaan peta dari garis 3x-5y+15=0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!

Jawaban : 

Pembahasan : 

22. Tentukan bayangan titik E(3, 7) jika direfleksikan terhadap sumbu x lalu dilanjutkan dengan dilatasi pada pusat (0, 0) dengan skala 2.

Pembahasan : 

E’(p, q) merupakan bayangan titik E jika direfleksikan terhadap sumbu x, maka

E’’(r, s) merupakan bayangan titik E’ jika dilatasikan pada pusat (0, 0) dengan skala 2.

Refleksi titik E pada sumbu x adalah

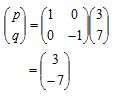
Dilatasi titik E’ pada pusat (0, 0) dengan skala 2 adalah

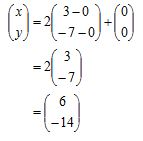
Jadi, bayangan titik E(3, 7) jika direfleksikan terhadap sumbu x lalu dilanjutkan dengan dilatasi pada pusat (0, 0) dengan skala 2 adalah (6, -14)