PENGALAMAN, SOAL, DAN PEMBAHASAN TRIGONOMETRI

TRIGONOMETRI

PENGALAMAN
Halo semuanya...


Perkenalkan nama saya Gathan Darmawan dari SMAN 63 Jakarta

Pada kesempatan kali ini saya akan bercerita tentang pengalaman saya saat mempelajari matematika

Siapa sih disini yang tidak kenal dengan mata pelajaran satu ini ? tentu saja dari kita semua pasti mengenal dengan pelajaran yang terkenal dengan rumit dan susahnya, ya Matematika. Berbicara tentang Matematika pasti banyak dari kalian yang kurang menyukai pelajaran tersebut kan ? termasuk saya sih. Mungkin karena hitung-hitungan ? atau karena banyak rumus-rumus yang harus dihafalkan ? atau mungkin ada hal lain ? tetapi terlepas dari itu semua sebenarnya Matematika pelajaran yang menyenangkan apabila kita suka dan mau menerima pelajaran itu dalam diri kita. Apabila kita berusaha dan ikhlas menerima pelajaran tersebut, maka kata "Sulit" tidak akan kita temukan lagi dalam setiap pembelajaran Matematika. Karena sejatinya tidak ada pelajaran yang tidak bisa kita pahami, tergantung dari kita-nya ikhlas dan mau menerima pelajaran itu atau tidak. 

Saya juga sama seperti kalian-kalian yang menilai bahwa Matematika itu sulit, karena memang dari awalnya saya berpikir bahwa "Matematika itu Sulit" dan dari pikiran tersebut maka akan terjadi sugesti bahwa Matematika itu memang sulit. Dan jika kita berpikir sebaliknya bahwa "Matematika itu Mudah" maka kita akan bersugesti bahwa Matematika memang mudah. Hal yang saya sulitkan ketika belajar Matematika adalah menghafal rumus-rumusnya, karena rumus-rumus dalam matematika sangat banyak. Tetapi apabila kita menghafalnya dengan senang, menonton video tentang Matematika atau trik-trik unik menghafal rumus, maka masalah tersebut dapat teratasi

Menurut saya pelajaran yang paling saya sukai dari Matematika yaitu Trigonometri, alasannya karena walaupun rumus didalam Trigonometri sangat banyak tetapi rumus-rumusnya mudah diingat dan dipahami. Dan apabila kita sudah hafal dengan rumus-rumus Trigonometri maka kita dengan mudahnya dapat mengerjakan soal-soal tentang Trigonometri

Saya rasa cukup untuk saya bercerita tentang Pengalaman Belajar Matematika saya, saya harap yang saya sampaikan dapat bermanfaat dan menjadikan motivasi kalian dalam belajar Matematika. Terima Kasih Semuanya! 

CONTOH SOAL DAN PEMBAHASAAN TRIGONOMETRI 

3.7 MENYELESAIKAN CARA MERUBAH SATUAN PENGUKURAN SUDUT  TRIGONOMETRI RADIAN KE DERAJAT, DERAJAT KE RADIAN

Contoh Soal 1 : 

Soal : ¼ putaran = ….. o (derajat) ? 

Jawab : 
1 putaran = 360o
½ putaran = 180o
¼ putaran = 90o


Contoh Soal 2 : 

Soal : 90o = ….. radian ?

Jawab : 

360o = 2 pi radian = 2(3,14) radian = 6,28 radian
180o = pi radian = 3,14 radian
90o = ½ pi radian = ½ (3,14) = 1,57


Contoh Soal 3 : 

Soal : 60 radian = ….. putaran ?

Jawab : 

6,28 radian = 1 putaran
60 radian/6,28 = 9,55 putaran


3.7 MENYELESAIKAN RASIO TRIGONOMETRI (SINUS,COSINUS,TANGEN,COSECAN,SECAN, DAN COTANGEN) PADA SEGITIGA SIKU-SIKU DAN SUDUT ISTIMEWA (60,30, 45)

Contoh Soal 1 : Pada gambar di samping segitiga siku-siku ABC dengan panjang a= 8 dan c= 10

Jawab : 

Nilai b dihitung dengan teorema Pythagoras
         

3.7  MENYELESAIKAN RASIO TRIGONOMETRI (SINUS,COSINUS, TANGEN,COSECAN, SECAN,DAN COTANGEN)PADA SEGITIGA SIKU-SIKU DI DALAM KOORDINAT KARTESIUS
Contoh Soal 1 : 
Segitiga siku-siku ABC mempunyai panjang sisi-sisinya a = 3, b = 4 dan c = 5. Carilah nilai dari keenam perbandingan trigonometri untuk sudut !
Jawab : 
Dengan menggunakan konsep yang diatas, diperoleh nilai 
sin A = sisi di hadapan sudut hipotenusa = a/c = 3/5
cos A = sisi di dekat sudut hipotenusa = b/c = 4/5
tan A = sin A/ cos A = a/b = 3/4
cosec A = 1/sin A = c/a = 5/3
sec A = 1/cos A = c/b = 5/4
cotan A = 1/tan A = b/a = 4/3

3.7 MENYELESAIKAN NILAI TRIGONOMETRI PADA SUATU SUDUT SEIGITGA SIKU-SIKU PADA KOORDINAT CARTESIUS

Contoh Soal 1 :  Jika sin α=5/13, dengan α sudut lancip, maka cos α...

Jawab :

Untuk mengerjakan soal seperti ini, buatkan dulu segitiga siku-sikunya. Panjang sisi yang belum diketahui bisa dicari dengan dalil phytagoras. Dari gambar terlihat jelas bahwa cos α = 12/13

3.7 MENYELESAIKAN KOMPOSISI OPERASI (+,-,:,∘ ) NILAI TRIGONOMETRI
Contoh Soal 1 : Tangen x = 1/V7. Tentukan nilai ((cosec^2(x)-sec^2(x))/(cosec^(x)+sec^2(x))

Jawab : 
Secan = sisi miring/sisi pada sudut
Cosecan = sisi miring / sisi di hadapan sudut
Secan (x) = V8/V7
Cosecan (x) = V8/1 atau V8
= ((V8)^2-(V8/V7)^2)/((V8)^2+(V8/V7)^2)
= (8 – 8/7)(8+8/7)
= (48/7)(64/7)
= 3072/49

3.7 MENYELESAIKAN SUDUT ELEVASI, SUDUT DEPRESI

Contoh Soal 1 :  Andi berdiri tegak pada jarak 10√3 m dari kaki sebuah pohon besar yang tumbuh gerak lurus. Jika tinggi Andi 1,6 m dan melihat ke puncak pohon dengan sudut elevasi 60°. Tentukan tinggi pohon tersebut?

Jawab : 





3.8 MENYELESAIKAN RASIO TRIGONOMETRI UNTUK SUDUT-SUDUT DI BERBAGAI KUADRAN 
Contoh Soal 1 : 
Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 50°
tan 40°
cos 35°
Jawab : 
sin 50° = sin (90° − 400°)
= cos 40°
tan 40° = tan (90° − 50°)
= cot 50°
cos 35° = cos (90° − 55°)
= sin 55°
Ketiganya bernilai positif, karena sudut 50°, 40° dan 35° berada di kuadran I.

Contoh Soal 2 : Berapa nilai sin 120o?

 Jawab : 120 = 90 + 30, jadi sin 120o dapat dihitung dengan
Sin 120o = Sin (90o + 30o) = Cos 30o (nilainya positif karena soalnya adalah sin 120o, di kuadran 2, maka hasilnya positif)

3.8 MENYELESAIKAN RASIO TRIGONOMETRI UNTUK SUDUT-SUDUT BERELASI (KUADRAN : I,II,III,IV), SUDUT NEGATIF, DAN SUDUT > 360 DERAJAT

Contoh Soal 1 : Nilai dari sin(−π/2) adalah…

Jawab : sin (−π/2)=−sin π/2=−sin 90o = −1

3.8 MENYELESAIKAN PERSAMAAN TRIGONOMETRI SEDERHANA ATAU PERSAMAAN IDENTITAS TRIGONOMETRI = RUMUS IDENTITAS TRIGONOMETRI 

Contoh Soal 1 :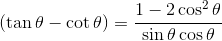 

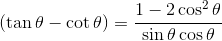
Jawab :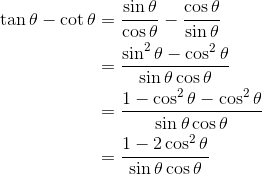 


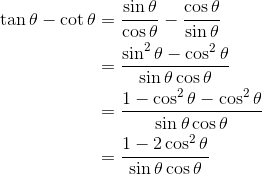
3.8 MENYELESAIKAN KOORDINAT KUTUB KE KOORDINAT CARTESIUS, KOORDINAT CARTESIUS KE KOORDINAT KUTUB 

Contoh Soal 1 :  Konversikan koordinat kartesius P (4,-3) menjadi koordinat kutub!

Jawab : Diketahui:  x = 4 dan y = -3
maka r = √x²+y² = √4²+(-3)² = √25 = 5
           α = tan^-1 (y/x) = tan^-1 (-3/4)
              = -36,69 ° atau -37°

Contoh Soal 2 : Konversikan koordinat kutub P (10,60°) menjadi koordinat kartesius!

Jawab : 
Diketahui:  r = 10 dan α = 60°
maka x = r . Cos α = 10 . cos 60°
               = 10 . 1/2= 5
dan    y = r . Sin α = 10 . Sin 60°
               = 10 . 1/2√3= 5√3
Jadi koordinat kartesiusnya (5, 5√3).


3.8 MENYELESAIKAN SOAL CERITA PERBANDINGAN TRIGONOMETRI 
Contoh Soal 1 : Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan kecepatan 40 km/jam selama 2 jam dengan arah 030°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2,5 jam dengan arah 150°. Buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!

Jawab : 

Jarak = kecepatan x waktu
Jarak pelabuhan A ke B adalah 40 x 2 = 80 km
Jarak pelabuhan B ke C adalah 60 x 2,5 = 150 km

Perhatikan gambar terlampir.
Besar sudut ABC adalah 30° + 30° = 60°
Gunakan aturan cosinus untuk mencari AC

AC² = AB² + BC² - [2 x AB x BC x cos ∠ABC]
AC² = 80² + 150² - [2 x 80 x 150 x cos 60°]
AC² = 28.900 - [2 x 80 x 150 x ¹/₂]
AC² = 28.900 - 12.000
AC = √ 16.900
Diperoleh jarak antara pelabuhan A dan C sejauh 130 km

3.9 MENYELESAIKAN ATURAN SINUS DIKETAHUI 2 SUDUT DAN 1 SISI 
Contoh Soal 1 : 
Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!

Jawab : 
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm

3.9 MENYELESAIKAN ATURAN SINUS DIKETAHUI 1 SUDUT DAN 2 SISI 

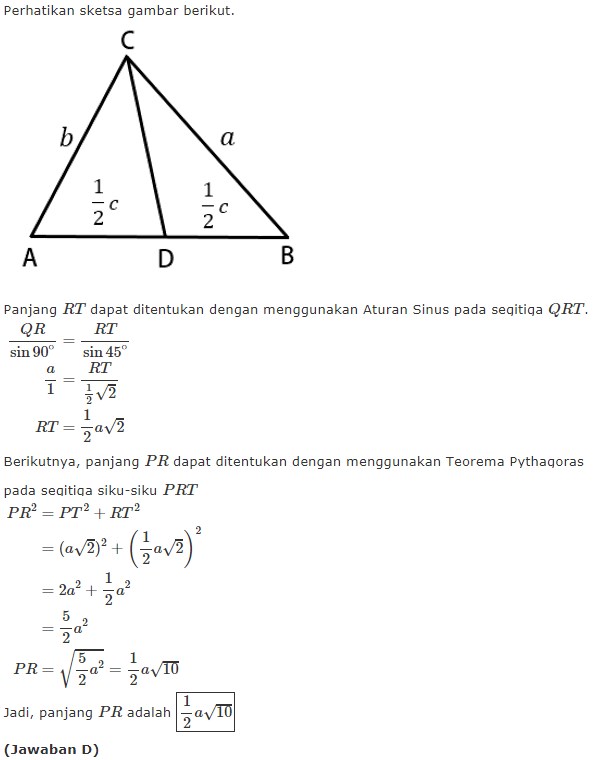
 Contoh Soal 1 : Pada △ P Q R , diketahui besar ∠ Q = 45° dan garis tinggi dari titik R . Jika Q R = a dan P T = a √ 2 , maka panjang P R adalah...

 Jawab : jawaban soal aturan sinus dan cosinus no 7

3.9 MENYELESAIKAN ATURAN COS DITANYA SISI 

Contoh Soal 1 : Sebuah segitiga ABC memiliki sisi dengan panjang a = 10 cm, c = 12 cm, besar sudut B = 60°. Hitung panjang sisi b!

Jawab : b2 = a2+ c2 – 2ac cos B
             b2 = 100+144 – 44 cos 60̊
             b2 = 244 – 44(0,5)
             b2 = 244 – 22
             b2 = 222
               b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm

3.9 MENYELESAIKAN ATURAN COS DITANYA SUDUT 

Contoh Soal 1 : AB = 20 cm, BC = 10√3 cm dan AC = 10 cm. Tentukan besar ∠A

 
Jawab : Dengan aturan kosinus pada ΔABC diperoleh nilai sudut A:
  


3.9 MENYELESAIKAN LUAS SEGITIGA JIKA DIKETAHUI : 1 SUDUT 2 SISI, 3 SISI, 2 SUDUT 1 SISI 

Contoh Soal 1 :  Berapa panjang sisi AC ?
Jawab : 
AB = c dan AC = b
besar <C = 180° - (75°+ 60°) = 45°
  b     =      c  
Sin B      Sin C
  b         =     20  
Sin 60°     Sin 45°
b  =  20 x Sin 60°  =   20 x  ½√3
            Sin 45°               ½√2
b  =  20√3  x √2    =   10√6cm
           √2      √2

3.10 MENYELESAIKAN GAMBAR FUNGSI TRIGONOMETRI F(X) = SIN X, F(X) = COS X, F(X) = TAN X, F(X) = CSC X, F(X) = SEC X, F(X) = COT X 

Contoh Soal 1 : Tentukan turunan dari y = sin 6x !

Jawab : 
Misalkan : u = 6x   ⇒   u’ = 6
y’ = cos u . u’
y’ = cos 6x . 6
y’ = 6cos 6x

Contoh Soal 2 : Tentukan turunan dari y = cos x2









Jawab : 






 Misalkan : u = x2   ⇒   u’ = 2x
y’ = −sin u . u’
y’ = −sin x2  . 2x
y’ = −2x sin x2


3.10 MENYELESAIKAN MEMBACA GAMBAR FUNGSI TRIGONOMETRI F(X) = SIN X, F(X) = COS X, F(X) = TAN X, F(X) = CSC X, F(X) = SEC X, F(X) = COT X 

Contoh Soal 1 : Diketahui f(x) = sin(cos x)

Jawab : f"(x) = - (cos x) . (cos (cos x)) – (sin x) . (sin x) . (sin (cos x))

Contoh Soal 2 : Temukan turunan pertama dari f (x) = tan x + Sec x

Jawab : f''(x) = sec 2x + Sec  x tan x = Sec x ( Sec x + tan x)

3.10 MENYELESAIKAN RANGE NILAI FUNGSI TRIGONOMETRI F(X) = SIN X, F(X) = COS X, F(X) = TAN X, F(X) = CSC X, F(X) = SEC X, F(X) = COT X 

Contoh Soal 1 :  Turunan pertama dari f(x) = 7 cos (5 – 3x) adalah f ‘ (x) =  …..
  • 35 sin (5 – 3x)
  • – 15 sin (5 – 3x)
Jawab : 
ingat, 
maka, 










3.10 MENYELESAIKAN FUNGSI TRIGONOMETRI DENGAN MENGGUNAKAN LINGKARAN SATUAN UNTUK MENENTUKAN PERIODE MAKSIMUM DAN MINIMUM

Contoh Soal 1 : 
Tentukan nilai maksimum dan minimum fungsi 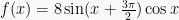f(x) = 8\sin (x+\frac{3\pi}{2}) \cos x

Jawab : 
Gunakan :2\sin a \cos \beta = \sin(a + \beta) + \sin (a - \beta)
f(x) = 8\sin(x+\frac{3\pi}{2}) \cos xf(x) = 4 \times 2\sin(x+\frac{3\pi}{2}) \cos x
f(x) = 4(\sin(x+\frac{3\pi}{2} - x))
f(x) = 4(\sin(2x+\frac{3\pi}{2}) + \sin(\frac{\pi}{2})) = 4(\sin(2x+\frac{3\pi}{2}) - 1)
f(x) = 4\sin (2x+\frac{3\pi}{2}) - 4
Sehingga :
  • Untuk sin⁡(2x +\frac{3\pi}{2}) = 1, maka f_{maks} = 4(1) - 4 = 0
  • Untuk sin⁡(2x+\frac{3\pi}{2}) = -1, maka f_{min} = 4(-1) - 4 = -8













Komentar

  1. fransiskaokt11 Mei 2020 pukul 01.24

    Komentar ini telah dihapus oleh pengarang.

    BalasHapus
  2. fransiskaokt11 Mei 2020 pukul 01.26

    Komentar ini telah dihapus oleh pengarang.

    BalasHapus
  3. fransiskaokt11 Mei 2020 pukul 01.26

    Soalnya mantep ya 👍. Boleh di copy paste kah?? 😁

    BalasHapus
    Balasan
    1. Gathan Darmawan11 Mei 2020 pukul 01.38

      Jelas sangat mantep, ohh iyaa silahkan sahabat!

      Hapus

Posting Komentar

Postingan populer dari blog ini

NILAI STASIONER, FUNGSI NAIK DAN FUNGSI TURUN

Gambar
Nama : Gathan Darmawan (13)  Kelas : XI IPS 3  NILAI STASIONER, FUNGSI NAIK DAN FUNGSI TURUN Fungsi naik ,  fungsi turun , dan  fungsi diam (stasioner)  merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Kondisi yang dimaksud dapat berupa berikut. Jika  f ′ ( x ) f ′ ( x )  bertanda positif, atau  f ′ ( x ) > 0 f ′ ( x ) > 0 , maka kurva fungsi dalam keadaan naik (disebut fungsi naik). Jika  f ′ ( x ) f ′ ( x )  bertanda negatif, atau  f ′ ( x ) < 0 f ′ ( x ) < 0 , maka kurva fungsi dalam keadaan turun (disebut fungsi turun). Jika  f ′ ( x ) f ′ ( x )  bertanda netral, atau  f ′ ( x ) = 0 f ′ ( x ) = 0 , maka kurva fungsi dalam keadaan tidak turun dan tidak naik, istilahnya kita sebut sebagai stasioner (disebut juga fungsi diam). Kondisi suatu fungsi  y = f ( x ) y = f ( x )  dalam keadaan naik, turun, atau diam Diberikan fungsi  y = f ( x ) y = f ( x )  dalam interval  I I  dengan  f ( x ) f ( x )  diferensiabel (dapat diturunkan) pada setiap
Baca selengkapnya

SOAL DAN PEMBAHASAN TRIGONOMETRI

Gambar
NAMA : GATHAN DARMAWAN (14) KELAS : X IPS 3 TUGAS : MATEMATIKA 3.7 MENYELESAIKAN CARA MERUBAH SATUAN PENGUKURAN SUDUT  TRIGONOMETRI RADIAN KE DERAJAT, DERAJAT KE RADIAN Contoh Soal 1 :  Soal :  ¼ putaran = …..  o  (derajat) ?   Jawab :   1 putaran = 360 o ½ putaran = 180 o ¼ putaran = 90 o Contoh Soal 2 :  Soal :  90 o  = ….. radian ? Jawab :  360 o  = 2 pi radian = 2(3,14) radian = 6,28 radian 180 o  = pi radian = 3,14 radian 90 o  = ½ pi radian = ½ (3,14) = 1,57 Contoh Soal 3 :  Soal :  60 radian = ….. putaran ? Jawab :  6,28 radian = 1 putaran 60 radian/6,28 = 9,55 putaran 3.7   MENYELESAIKAN RASIO TRIGONOMETRI (SINUS,COSINUS,TANGEN,COSECAN,SECAN, DAN COTANGEN) PADA SEGITIGA SIKU-SIKU DAN SUDUT ISTIMEWA (60,30, 45) Contoh Soal 1 :  Pada gambar di samping segitiga siku - siku ABC dengan panjang  a =   8  dan  c =   10 Jawab :  Nilai  b  dihitung dengan teorema Pythagoras           3.7   MENYE
Baca selengkapnya