INTEGRAL TERTENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA
Nama : Gathan Darmawan (13)
Kelas : XI IPS 3
INTEGRAL TERTENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA
Integral tentu
Pada bahasan sebelumnya, telah dijelaskan tentang integral tak tentu di mana hasil dari integrasinya masih berupa fungsi. Jika hasil integrasinya berupa nilai tertentu, integralnya disebut integral tentu. Adapun bentuk umum integral tentu adalah sebagai berikut. 
dengan: x = a disebut batas bawah
x = b disebut batas atas
Arti dari bentuk integral di atas adalah suatu f’(x) diintegralkan atau dijumlahkan secara kontinu mulai dari titik a sampai titik b, sehingga hasil akhir yang diperoleh akan berupa angka, tidak lagi fungsi.
a. Sifat-sifat Integral Tentu
Apabila f(x), g(x) terdefinisi pada selang a, b, maka diperoleh persamaan berikut.
1. 
2. 
3. 
4. 
5. 
b. Aplikasi Integral Tentu
Seperti Quipperian ketahui bahwa integral bisa diaplikasikan dalam kehidupan sehari-hari. Salah satu contoh yang umum dikenal adalah luas daerah. Luas daerah yang dimaksud adalah luas daerah di bawah kurva. Adapun langkah menghitungnya adalah sebagai berikut.
- Batas daerah yang akan diintegralkan harus jelas. Adapun batas daerah yang dimaksud adalah batas kiri dan kanannya serta batas atas dan bawahnya. Bentuk batas daerah bisa berupa fungsi atau konstanta, fungsi linier dan nonlinier (kuadrat, pangkat 3, akar pangkat). Bagaimana jika salah satu batas belum diketahui? Quipperian harus mencarinya terlebih dahulu, agar luasnya bisa dihitung.
- Quipperian harus mampu menggambar daerah di dalam kurva sesuai dengan batas-batas yang telah ditentukan (jika gambar masih dinyatakan dalam batas-batasnya saja). Oleh karena itu, diperlukan kemampuan untuk menggambar dengan baik.
- Quipperian juga harus bisa menempatkan rumus yang tepat untuk menghitung luas daerah berdasarkan ketentuan yang telah ada. Jangan lupa untuk memperhatikan gambar daerah dan rumus yang bersesuaian. Quipperian jangan khawatir ya, setiap daerah memiliki rumus fungsinya masing-masing, contohnya berikut ini.
a) Bentuk daerah jenis 1
b) Bentuk daerah jenis 2
c) Rumus cepat mencari luas
Rumus cepat tidak berlaku untuk seluruh daerah ya, Quipperian. Rumus ini berlaku pada daerah-daerah yang memiliki kondisi berikut.
- Memiliki dua batas fungsi, yaitu fungsi kuadrat dan fungsi kuadrat.
- Memiliki dua batas fungsi, yaitu fungsi kuadrat dan fungsi linear.
Jika memenuhi dua kondisi di atas, luasnya dapat dicari menggunakan persamaan berikut.
Lalu, apa yang dimaksud dengan a, b, dan c? Ketiga konstanta tersebut diperoleh dari proses berikut.
- Jika fungsinya y = f(x) dan y = g(x), maka buat fungsi selisihnya y = f(x) – g(x).
Jika fungsinya y = f(y) dan y = g(y), maka buat fungsi selisihnya y = f(y) – g(y)
- Fungsi selisih yang sudah Quipperian dapatkan, jangan disederhanakan lagi agar teridentifikasi nilai a, b, dan c.
- Jika Quipperian sudah mendapatkan nilai a, b¸ dan c, substitusikan ke persamaan luas berikut.

CONTOH SOAL
1. Carilah hasil dari ʃ21 6x2 dx !
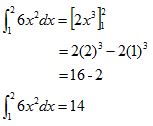
Jadi, hasil dari ʃ21 6x2 dx adalah 14.
2. Tentukan hasil integral tentu dari ʃ-1-4 7 dx !
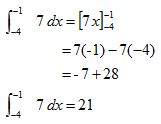
Jadi, hasil integral tentu dari ʃ-1-4 7 dx adalah 21.
3. Berapakah nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx ?
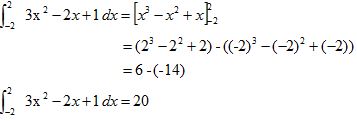
Jadi, nilai integral tentu dari ʃ-2-2 3x2 – 2x + 1 dx adalah 20.
4. Hitunglah nilai integral tentu dari ʃ94 1/√x dx !
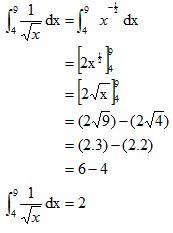
Jadi, nilai integral tentu dari ʃ94 1/√x dx adalah 2.
5. Carilah hasil integral tentu dari ʃπ/3π/6 cos x dx
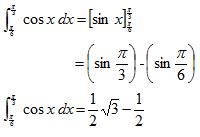
Jadi, hasil integral tentu dari ʃπ/3π/6 cos x dx adalah ½ √3 – ½.
6. Tentukan hasil integral tentu dari ʃπ/20 cos x + sin x dx
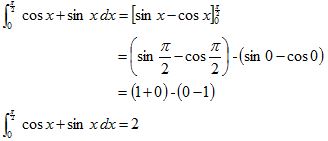
Jadi, hasil integral tentu dari ʃπ/20 cos x + sin xdx adalah 2.
7. Diketahui ʃp1 2x – 4 dx = -1, berapakah nilai 7p?
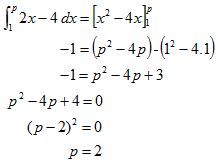
Jadi nilai dari 7p adalah 14.
Komentar
Posting Komentar