MENGGAMBAR GRAFIK FUNGSI DENGAN TURUNAN PERTAMA DAN TURUNAN KEDUA

Nama : Gathan Darmawan (13) 

Kelas : XI IPS 3 

PEMBAHASAN YANG BERHUBUNGAN DENGAN TURUNAN PERTAMA DAN TURUNAN KEDUA BESERTA CONTOH SOALNYA

Postingan ini membahas contoh soal fungsi kuadrat dan pembahasannya + jawabannya. Lalu apa itu fungsi kuadrat ?. Suatu fungsi f pada himpunan bilangan real (R) yang ditentukan oleh f(x) = ax2 + bx + c dengan a, b, c ∈ R dan a ≠ 0 disebut fungsi kuadrat. Ada dua cara menggambar grafik fungsi kuadrat yaitu dengan menggunakan tabel koordinat bebarapa titik dan menggunakan titik-titik penting yang dilalui grafik. Titik-titik penting tersebut adalah titik potong grafik dengan sumbu X, titik potong grafik dengan sumbu Y dan titik balik.

Berdasarkan nilai diskriminannya (D = b2 – 4ac), grafik fungsi kuadrat (y = ax2 + bx + c) ) terdiri dari 6 kemungkinan yaitu sebagai berikut.

1. Jika a > 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik yang berbeda. Jenis titik baliknya minimum.
2. Jika a > 0 dan D = 0, grafik fungsi kuadrat memotong sumbu X di satu titik atau menyinggung sumbu X. Jenis titik baliknya minimum.
3. Jika a > 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit positif). Jenis titik baliknya minimum.
4. Jika a < 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik berbeda. Jenis titik baliknya maksimum.
5. Jika a < 0 dan D = 0, grafik fungsi kuadrat menyinggung sumbu X dan titik baliknya maksimum.
6. Jika a < 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit negatif) dan titik balinya maksimum

CONTOH 

1. Perhatikan gambar fungsi kuadrat dibawah ini.

Persamaan fungsi kuadrat grafik diatas adalah…

A. y = x2 – 2x + 15 

B. y = x2 – 2x – 15 

C. y = x2 + 2x + 15 

D. y = x2 – 8x – 15

E. y = x2 – 8x + 15

Pembahasan / penyelesaian soal

Berdasarkan grafik fungsi kuadrat diatas kita ketahui:

x1 = -5

x2 = -3

y = 15

Fungsi kuadrat dibentuk dengan cara sebagai berikut:

y = a (x – x1) (x – x2)

y = a (x – (-5)) (x – (-3))

y = a (x + 5) (x + 3)

y = a (x2 + 3x + 5 x + 15)

y = a (x2 + 8x + 15)

Selanjutnya kita tentukan nilai a dengan subtitusi nilai x = 0 dan y = 15 sehingga didapat:

15 = a (02 + 8 . 0 + 15)

15 = a . 15

a = 15/15 = 1

Jadi fungsi kuadratnya adalah:

y = 1 (x2 + 8x + 15)

y = x2 + 8x + 15

Jadi soal ini jawabannya C.

2.

Persamaan fungsi kuadrat grafik diatas adalah…

A. y = 2x2 + 2x – 4 

B. y = 2x2 – 2x – 4 

C. y = x2 + x – 4

D. y = x2 – 2x – 4 

E. y = x2 – x – 4

Pembahasan / penyelesaian soal

Berdasarkan grafik diatas kita ketahui:

x1 = -1

x2 = 2

y = -4

Maka persamaan fungsi kuadrat sebagai berikut:

y = a (x – (-1)) (x – 2)

y = a (x + 1) (x – 2)

y = a (x2 – x – 2)

Menentukan nilai a dengan cara subtitusi x = 0 dan y = -4 sehingga didapat hasil dibawah ini:

-4 = a (02 – 0 – 2)

-4 = a . -2

a = -4/-2 = 2

Sehingga persamaan kuadratnya adalah:

y = 2 (x2 – x – 2)

y = 2x2 – 2x – 4

Soal ini jawabannya B.

3. Perhatikan gambar dibawah ini.

Jika fungsi kuadrat grafik diatas dinyatakan oleh f(x) = ax2 + bx + c maka pernyataan dibawah ini yang benar adalah…

A. a < 0, b < 0, dan c < 0 

B. a < 0, b > 0 dan c > 0 

C. a < 0, b > 0 dan c < 0 

D. a > 0, b < 0 dan c > 0 

E. a > 0, b < 0 dan c < 0

Pembahasan / penyelesaian soal

Untuk menjawab soal ini kita bentuk terlebih dahulu persamaan fungsi kuadrat grafik diatas sebagai berikut:

y = a (x – (-3)) (x – (-1))

y = a (x + 3) (x + 1)

y = a (x2 + 4x + 3)

-3 = a (02 + 4 . 0 + 3)

-3 = a . 3

a = -3/3 = -1

y = -1 (x2 + 4x + 3)

y = -x2 – 4x – 3

Berdasarkan persamaan fungsi kuadrat diatas kita ketahui a = -1, b = -4 dan c = -3 atau a < 0, b < 0 dan c < 0. Jadi jawaban soal ini adalah A.

4. Perhatikan gambar dibawah ini.

Koordinat titik potong grafik dengan sumbu X adalah…

A. (-1, 0) dan (-8, 0)

B. (-1, 0) dan (8, 0) 

C. (1, 0) dan (-8, 0) 

D. (1, 0) dan (8, 0) 

E. (2, 0) dan (5, 0)

Pembahasan / penyelesaian soal

Berdasarkan grafik fungsi kuadrat diatas kita ketahui:

titik balik xp = 9/2

titik balik yp = -49/4

y = 8

xp = -b/2 . a = 9/2

 

Sehingga kita dapat a = 2/2 = 1 dan b = -9. 

yp = -(b2 – 4 . a . c)/4 . a = -49/4

 b2 – 4 . a . c = 49 

92 – 4 . 1 . c = 49 

81 – 4c = 49 atau 4c = 81 – 49 = 32 

c = 32/4 = 8 

Jadi persamaan fungsi kuadrat grafik diatas adalah: 

y = ax2 + bx + c 

y = xp – 9x + c 

Untuk menentukan titik potong x kita lakukan pemfaktoran sebagai berikut: 

xp – 9x + 8 = 0 

(x1 – 8) (x2 – 1) = 0 

x1 = 8 dan x2 = 1

Jadi titik potong sumbu X adalah (8,0) dan (1,0). Soal ini jawabannya D.

5. Diketahui jumlah 2 bilangan adalah 72. Hasil kali maksimum kedua bilangan adalah…

A. 72 

B. 144 

C. 360 

D. 1.296 

E. 5.184

Pembahasan / penyelesaian soal

Untuk menjawab soal ini kita lalukan pemisalan 2 bilangan yaitu x dan y sehingga kita peroleh:

x + y = 72

y = 72 – x

x . y = x (72 – x) = 72x – x2

K = -x2 + 72x

Berdasarkan fungsi kuadrat diatas kita ketahui a = -1, b = 72 dan c = 0. Hasil kali maksimum kita gunakan rumus dibawah ini:

K = -(b2 – 4 . a . c)/4 . a

 K = -(722 – 4 . -1 . 0)/4 . -1 = 5184/4= 1296

Jadi soal ini jawabannya D.

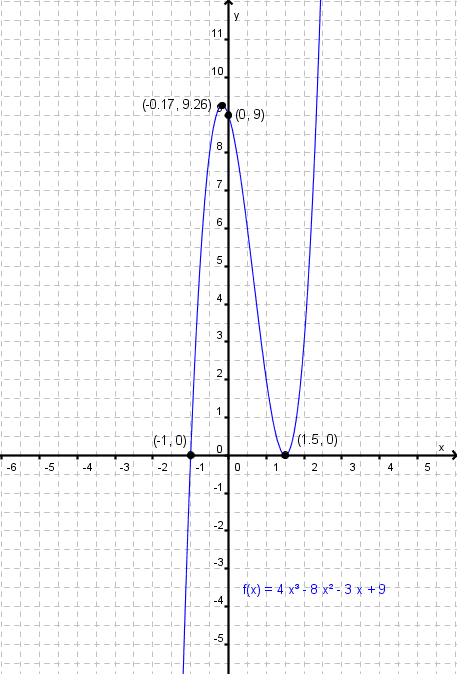
Gambarlah sketsa kurva y = f(x) = 4x3 – 8x2 – 3x + 9.

Jawab :

Untuk menyelesaikannya, mari kita pakai langkah-langkah yang sudah dibahas di atas :

Langkah 1

Titik potong dengan sumbu Y, di perloeh apabila x = 0.

y = f(0) = 4(0)3– 8(0)2 – 3(0) + 9 = 9 . Maka Titik potongnya adalah (0,9)

Titik potong dengan sumbu X, diperoleh bila y = 0.

Berarti, 4x3 – 8x2  – 3x + 9 = 0 . Untuk mendapatkan nilai x, pakailah teorema faktor yang sudah dipelajari pada pokok bahasan polinom atau suku banyak. Maka akan didapat x = -1 atau x = 1,5. Maka demikian titik potong dengan sumbu X ialah (-1,0) dan (1,5;0)

Cari turunan pertama dan kedua.

f1(x) = 12x2 – 16x – 3

f11(x) = 24x – 16

Fungsi naik, fungsi turun, dan titik ekstrim.

Fungsi f naik bila f'(x) > 0

12×2 – 16x – 3 > 0

(2x-3) (6x+1) > 0

x < -1/6 atau x > 1,5

Fungsi f turun bila f'(x) < 0

12×2 – 16x – 3 < 0

(2x-3)(6x+1) < 0

-1/6 < x < 1,5

Titik ekstrim didapatkan apabila f'(x) = 0

12×2 – 16x – 3 = 0

(2x-3)(6x+1) = 0

x = -1/6 atau x = 1,5

x = -1/6 pada bentuk desimal dapat ditulis sebagai x = -0,17

Jenis stasioner bisa diperoleh dengan substitusi x ketika f'(x) = 0 ke f”(x).

f”(-1/6) = 24(-1/6) – 16 = -20 < 0

menurut uji turunan kedua, x = -1/6 memiliki nilai balik maksimum. Nilai balik maksimumnya didapatkan dengan substitusi nilai x ke fungsi awal .

f(-1/6) = 9 7/27 = 9,26

f”(1,5) = 24(1,5) – 16 = 20 > 0

menurut uji turunan kedua, x = 1,5 memiliki nilai balik minimum. Nilai balik minimumnya didapatkan dengan substitusi nilai x ke fungsi awal.

f(1,5) = 0

Kecekungan fungsi dan titik belok fungsi.

Fungsi f cekung ke atas bila f”(x) > 0

24x – 16 > 0

24x > 16

x > 2/3

Fungsi f cekung ke bawah bila f”(x) < 0

24x – 16 < 0

24x < 16

x < 2/3

Titik belok fungsi f didapatkan bila f”(x) = 0

24x – 16 = 0

24x = 16

x = 2/3

f(2/3)=4 17/27

Titik beloknya adalah (2/3,4 17/27)

Langkah 2 :

Gambarlah titik-titik yang didapatkan pada langkah 1 pada koordinat kartesius. Titik-titik tersebut yaitu sebagai berikut. :

(0,9), (-1,0), (1,5;0), (-1/6,9 7/27), dan (2/3,4 17/27)

Langkah 3 :

Hubungkan titik-titik yang sudah diletakan pada koordinat kartesius pada kurva halus dengan memperhatikan naik-turun dan kecekungannya, sehingga didapatkan grafik seperti dibawah ini :

DAFTAR PUSTAKA : 

https://www.pelajaran.co.id/2017/16/menggunakan-konsep-turunan-dalam-menggambar-kurva-polinom.html