SOAL DAN PEMBAHASAN TRIGONOMETRI
NAMA : GATHAN DARMAWAN (14)
¼ putaran = 90o



KELAS : X IPS 3
TUGAS : MATEMATIKA
3.7 MENYELESAIKAN CARA MERUBAH SATUAN PENGUKURAN SUDUT TRIGONOMETRI RADIAN KE DERAJAT, DERAJAT KE RADIAN
Contoh Soal 1 :
Soal : ¼ putaran = ….. o (derajat) ?
Jawab :
1 putaran = 360o
½ putaran = 180o¼ putaran = 90o
Contoh Soal 2 :
Soal : 90o = ….. radian ?
Jawab :
360o = 2 pi radian = 2(3,14) radian = 6,28 radian
180o = pi radian = 3,14 radian
90o = ½ pi radian = ½ (3,14) = 1,57
180o = pi radian = 3,14 radian
90o = ½ pi radian = ½ (3,14) = 1,57
Contoh Soal 3 :
Soal : 60 radian = ….. putaran ?
Jawab :
6,28 radian = 1 putaran
60 radian/6,28 = 9,55 putaran
60 radian/6,28 = 9,55 putaran
3.7 MENYELESAIKAN RASIO TRIGONOMETRI (SINUS,COSINUS,TANGEN,COSECAN,SECAN, DAN COTANGEN) PADA SEGITIGA SIKU-SIKU DAN SUDUT ISTIMEWA (60,30, 45)
Contoh Soal 1 : Pada gambar di samping segitiga siku-siku ABC dengan panjang a= 8 dan c= 10
Jawab :
Nilai b dihitung dengan teorema Pythagoras
3.7 MENYELESAIKAN RASIO TRIGONOMETRI (SINUS,COSINUS, TANGEN,COSECAN, SECAN,DAN COTANGEN)PADA SEGITIGA SIKU-SIKU DI DALAM KOORDINAT KARTESIUS
Contoh Soal 1 :
Segitiga siku-siku ABC mempunyai panjang sisi-sisinya a = 3, b = 4 dan c = 5. Carilah nilai dari
keenam perbandingan trigonometri untuk sudut !
Jawab :
Dengan menggunakan konsep yang diatas, diperoleh nilai
sin A =
sisi di hadapan sudut
hipotenusa =
a/c = 3/5
cos A =
sisi di dekat sudut
hipotenusa =
b/c =
4/5
tan A =
sin A/ cos A =
a/b = 3/4
cosec A =
1/sin A =
c/a =
5/3
sec A =
1/cos A =
c/b =
5/4
cotan A =
1/tan A =
b/a =
4/3
3.7 MENYELESAIKAN KOMPOSISI OPERASI (+,-,:,∘ ) NILAI TRIGONOMETRI
Contoh Soal 1 : Tangen x = 1/V7. Tentukan nilai ((cosec^2(x)-sec^2(x))/(cosec^(x)+sec^2(x))
Jawab :
Secan = sisi miring/sisi pada sudut
Cosecan = sisi miring / sisi di hadapan sudut
Secan (x) = V8/V7
Cosecan (x) = V8/1 atau V8
= ((V8)^2-(V8/V7)^2)/((V8)^2+(V8/V7)^2)
= (8 – 8/7)(8+8/7)
= (48/7)(64/7)
= 3072/49
3.8 MENYELESAIKAN RASIO TRIGONOMETRI UNTUK SUDUT-SUDUT DI BERBAGAI KUADRAN
Contoh Soal 1 :
Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 50°
tan 40°
cos 35°
Jawab :
sin 50° = sin (90° − 400°)
= cos 40°
tan 40° = tan (90° − 50°)
= cot 50°
cos 35° = cos (90° − 55°)
= sin 55°
Ketiganya bernilai positif, karena sudut 50°, 40° dan 35° berada di kuadran I.
3.8 MENYELESAIKAN SOAL CERITA PERBANDINGAN TRIGONOMETRI
Contoh Soal 1 : Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan kecepatan 40 km/jam selama 2 jam dengan arah 030°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2,5 jam dengan arah 150°. Buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!
Jawab :
Jarak = kecepatan x waktu
Jarak pelabuhan A ke B adalah 40 x 2 = 80 km
Jarak pelabuhan B ke C adalah 60 x 2,5 = 150 km
Perhatikan gambar terlampir.
Besar sudut ABC adalah 30° + 30° = 60°
Gunakan aturan cosinus untuk mencari AC
AC² = AB² + BC² - [2 x AB x BC x cos ∠ABC]
AC² = 80² + 150² - [2 x 80 x 150 x cos 60°]
AC² = 28.900 - [2 x 80 x 150 x ¹/₂]
AC² = 28.900 - 12.000
AC = √ 16.900
Diperoleh jarak antara pelabuhan A dan C sejauh 130 km
3.9 MENYELESAIKAN ATURAN SINUS DIKETAHUI 2 SUDUT DAN 1 SISI
Contoh Soal 1 :
Diketahui sebuah segitiga PQR memiliki luas sebesar 96cm2. Jika panjang PR = 12cm dan besar ∠PRQ = 60o, tentukan panjang QR!
Jawab :
L = ½ × PR × QR × Sin ∠PRQ
96cm2 = ½ × 12cm × QR × Sin 60o
96cm2 = ½ × 12cm × QR × ½√3
96cm2 = 4√3cm × QR
QR = 96cm2 ÷ 4√3cm
QR = 24/√3 cm
QR = 8√3cm
Jadi, panjang QR adalah 8√3cm
3.10 MENYELESAIKAN FUNGSI TRIGONOMETRI DENGAN MENGGUNAKAN LINGKARAN SATUAN UNTUK MENENTUKAN PERIODE MAKSIMUM DAN MINIMUM
Contoh Soal 1 :
Tentukan nilai maksimum dan minimum fungsi 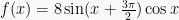
Jawab :
Gunakan :
Sehingga :
- Untuk sin
, maka
- Untuk sin
, maka

Komentar
Posting Komentar